PID Tuning Using Ziegler-Nichols Method

Introduction

PID controllers play a crucial role in industrial automation by regulating process variables such as temperature, pressure, flow rate, and speed. However, achieving optimal performance requires proper tuning of the PID parameters: proportional gain ((K_p)), integral time ((T_i)), and derivative time ((T_d)). One of the most commonly used empirical tuning methods is the Ziegler-Nichols method, which provides a systematic approach to obtaining PID parameters based on the system response.

The Ziegler-Nichols method was developed by John G. Ziegler and Nathaniel B. Nichols in the 1940s. It is widely adopted for tuning PID controllers due to its simplicity and effectiveness. This method is particularly useful for systems that exhibit first-order plus dead-time (FOPDT) behavior and is based on the process reaction curve or sustained oscillations.

Understanding the Ziegler-Nichols Method

The Ziegler-Nichols tuning method consists of two main approaches:

1. Step Response Method (Process Reaction Curve Method)
2. Continuous Cycling Method (Ultimate Sensitivity Method)

Each approach determines the PID parameters based on specific characteristics of the system’s response. The chosen method depends on whether a step input can be applied or if the system can be induced to oscillate.

Step Response Method (Process Reaction Curve Method)

This method is useful for systems where a step change can be applied, and the system’s transient response can be observed. The key idea is to measure the system’s response curve after a step input and extract important parameters such as delay time ((L)) and time constant ((T)).

Procedure

1. Apply a small step input to the system and observe the response.
2. Identify the delay time ((L))—the time before the output starts significantly changing.
3. Measure the time constant ((T))—the time taken to reach approximately 63% of the final value.
4. Calculate PID parameters using empirical formulas derived from system dynamics.

Tuning Rules

Using the Ziegler-Nichols tuning formulas, the PID parameters are estimated as follows:

• Proportional Controller (P): The gain is set as (K_p = \frac{1}{T}).
• Proportional-Integral Controller (PI): The proportional gain is reduced ((K_p = 0.9/T)), and integral action is introduced with (T_i = L/0.3).
• Proportional-Integral-Derivative Controller (PID): The proportional gain is set to (K_p = 1.2/T), the integral time to (T_i = 2L), and the derivative time to (T_d = 0.5L).

These values ensure a reasonably fast response while maintaining stability. However, further tuning may be required to fine-tune performance.

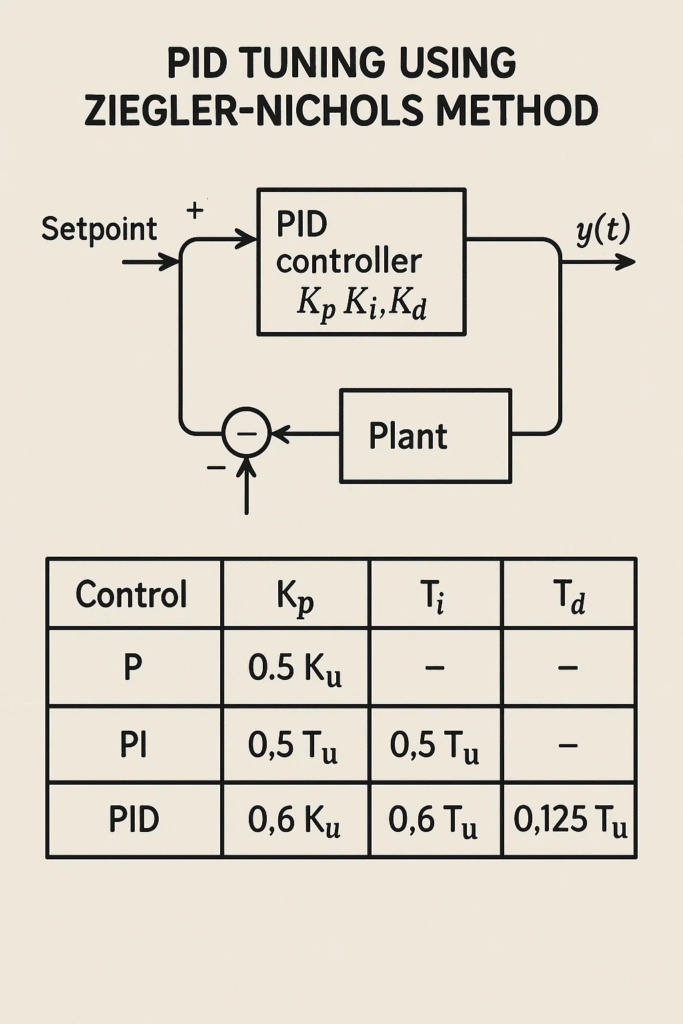
Continuous Cycling Method (Ultimate Sensitivity Method)

The Continuous Cycling Method is an alternative approach where the system is tested under proportional-only control to induce sustained oscillations. The goal is to determine the ultimate gain ((K_u)) and the ultimate period ((P_u)) by increasing the proportional gain until the system oscillates continuously.

Procedure

1. Disable integral and derivative control by setting (T_i) and (T_d) to infinity or turning them off.
2. Gradually increase (K_p) until the system exhibits stable, sustained oscillations.
3. Measure:
   • The ultimate gain ((K_u))—the proportional gain at sustained oscillation.
   • The ultimate period ((P_u))—the oscillation cycle duration.
4. Use empirical formulas to set PID parameters.

Tuning Rules

Ziegler-Nichols empirical equations for PID tuning in this method are:

• Proportional Controller (P): The gain is set as (K_p = 0.5K_u).
• Proportional-Integral Controller (PI): (K_p = 0.45K_u), (T_i = P_u / 1.2).
• Proportional-Integral-Derivative Controller (PID): (K_p = 0.6K_u), (T_i = P_u / 2), and (T_d = P_u / 8).

This method is aggressive, and adjustments may be needed to balance performance and stability.

Comparison of the Two Methods

The Step Response Method is easier to apply but provides less precise tuning compared to the Continuous Cycling Method, which requires sustained oscillations but achieves better precision. However, the Continuous Cycling Method can lead to instability in sensitive systems.

The choice of method depends on the system characteristics. Slow-response processes benefit from the Step Response Method, while well-behaved oscillatory systems may be better suited to the Continuous Cycling Method.

Challenges & Considerations in PID Tuning

Despite its effectiveness, the Ziegler-Nichols method has certain limitations:

1. System Stability:
   • The method often results in aggressive tuning, leading to overshoot or oscillations.
   • Fine adjustments might be needed to prevent instability.
2. Nonlinear or High-Order Systems:
   • The method assumes linear system behavior, which can degrade performance in nonlinear or complex systems.
   • Alternative tuning strategies such as Cohen-Coon, auto-tuning, or adaptive control may be needed.
3. Noise Sensitivity:
   • High derivative gain ((T_d)) can amplify noise, causing erratic control behavior.
   • Noise filtering strategies should be considered when using derivative control.
4. Alternative Tuning Methods:

• Methods such as Relay Feedback Tuning, Genetic Algorithms, and Neural Network-Based Tuning provide advanced options for optimizing PID control.

Conclusion

The Ziegler-Nichols method is an effective and straightforward approach to PID tuning. It provides a good initial estimate of PID parameters and works well for many industrial applications. However, the aggressive nature of this method means that fine-tuning is often necessary to achieve optimal performance.

While Ziegler-Nichols tuning helps set up a PID controller quickly, practitioners should combine empirical tuning with real-world observations and adjustments to enhance the stability and efficiency of their control systems.